FLEXSCHE

検索

検索

フレクシェ製品サイト

スタッフブログStaff Blog

  1. HOME > 
  2. 株式会社フレクシェ会社紹介特設サイト > 
  3. スタッフブログ > 
  4. 技術 > 
  5. 製品・サービス > 
  6. PGBattle2023マッシュマロ最終問をFLEXSCHEで解いてみた

PGBattle2023マッシュマロ最終問をFLEXSCHEで解いてみた

技術 製品・サービス

2024/03/25
written by CHO

CHO

本日は、PGBattle2023のマッシュマロ最終問題をtakt式で解いていきます。今さらPGBattle2023に関する記事を書くことについて、「時期を逸している」と感じる方もいらっしゃるかもしれません。しかし、様々な事情でこれまで手を付けることができなかったのです...

TL;DR

takt式は、少しの工夫を加えることで、

  • (多次元) 配列の操作

  • 再帰関数

  • (多重) Forループ

  • If文

などのプログラミング要素をすべて実現可能で、かなり複雑なアルゴリズムも扱えます。

問題と解説

問題文

与えられた文字列内で、隣り合う男女ペアを削除する問題です。削除できるのは隣接する男女のペアのみで、すべてのペアを削除しきれる場合の順列の数を求めます。

この問題の解法には「区間DP」（動的計画法）が用いられます。ネット上には多くの関連記事があり、その中で共通するのは再帰関数を活用したメモ化です。

基本戦略: 最後に選ばれる男女ペア (k, l) を再帰のトリガーとします。これにより、文字列を左・中央・右の3つの区間に分割し、それぞれの区間での解を計算します。

mashumaro_1.PNG

計算方法: 各区間を再帰的に呼び出し、その結果を元に[i, j]区間の解を組み立てます。各区間の組み合わせ数を乗じて、最終的な結果に加えます。組み合わせ数は事前に計算しておく必要があります。

実装の概要: C++とtaktの比較

1. 組み合わせ数の事前計算

c++

vvll Comb(N2+1, vll(N2+1, 1));
    for(int n = 1; n <= N2; n++) 
        for(int k=1; k <= n - 1; k++) 
            Comb[n][k] = (Comb[n-1][k-1] + Comb[n-1][k]) % MOD;

takt

$N2 := Math.Max($N.Div(2), 2),
$Comb := LongList.Make(1, ($N2 + 1) * ($N2 + 1), 0),
//_Print("N2: " + $N2 + String.LF),
$GetComb := (Long i, Long j)[$Comb.At($i * ($N2 + 1) + $j)]->Long,
$SetComb := (Long i, Long j, Long val)[$Comb.Set_( $i * ($N2 + 1) + $j, $val)],
_REP(2, $N2).ForEach([
    $m := $_object,
    _REP(1, $m - 1).ForEach([
        $k := $_object,
        $c := $GetComb($m - 1, $k - 1) + $GetComb($m - 1, $k),
        $c := $c.Nnmod($MOD),
        //_Print($m + " " + $k + " " + $c + String.LF),
        $SetComb($m, $k, $c),
    ]),
]),

実装のポイント

  • 二次元配列の利用: C++では二次元配列を用い、taktではこれを一次元配列として格納することで対応します。
  • 補助関数の使用: 取得や変更を簡単にするために、補助関数を定義します。
  • Forループの代替: C++のforループはtaktではLongList.ForEachを使って実現します。更に、計算式ライブラリをラッピングすることでコードの可読性を高めることができます。

2. メモ化DP

2.0 DPテーブルの定義

c++

vvll DP(N, vll(N, -1));

takt

$DP := LongList.Make(-1, $N * $N, 0),
$GetDP := (Long i, Long j)[$DP.At($i * $N + $j)]->Long,
$SetDP := (Long i, Long j, Long v)[$DP.Set_($i * $N + $j, $v)],

実装のポイント:

  • 二次元配列を使用し、組み合わせ数の計算時と同じアプローチを取ります。

2.1 メモ化再帰関数の定義

c++

function memoization = [&](ll i, ll j){
...
};

takt

$Memoization := (Long i, Long j)[
...
]->Long,

実装のポイント:

  • c++ のラムダ関数と同じく、taktでは関数定義により再帰関数も定義・利用できます。詳しくはtakt式マニアクス① をご参照ください。

2.1.1 最後に選ばれるペア (k, l) のループ

c++

for(int k = i; k <= j-1; k++) for(int l = k + 1; l <= j; l++){
...
}

takt

_REP($i, $j-1).ForEach([ $k := $_object, // k = i, ..., j-1
    _REP($k+1, $j).ForEach([ $l := $_object, // l = k+1, ..., j
    ])
]),

実装のポイント:

  • 多重ForループもLongList.ForEachを用いれば普通に使えます。

2.1.2 左・中央・右の3区間を再帰呼び出し

c++

if(k > i){
    memoization(i, k-1);
    left = (DP[i][k-1] * Comb[n2 - 1][nleft]) % MOD;
}
if(j > l){
    memoization(l+1, j);
    right = (DP[l+1][j] * Comb[n2 - 1 - nleft][nright]) % MOD;
}
if(l > k + 1){
    memoization(k+1, l-1);
    mid = DP[k+1][l-1] % MOD;
}

takt

$k > $i ? (
    $Memoization($i, $k - 1),
    $left := $GetDP($i, $k - 1) * $GetComb($len2 - 1, $nleft),
    $left := $left.Nnmod($MOD),
1 ): 0,
$j > $l ? (
    $Memoization($l + 1, $j),
    $right := $GetDP($l + 1, $j) * $GetComb($len2 - 1 - $nleft, $nright),
    $right := $right.Nnmod($MOD),
1 ): 0,
$l > $k + 1? (
    $Memoization($k + 1, $l - 1),
    $mid := $GetDP($k + 1, $l - 1).Nnmod($MOD),
1 ): 0,

実装のポイント:

  • if文は三項演算子を使用して表現できます。例: if(state) {}'' はstate ? () : 0,'' と書き換えます。
  • 整数の除算はLong.Divで行い、余剰はLong.Modで計算します。

2.1.3 結果への加算

c++

res = (res + ((left * mid) % MOD * right) % MOD) % MOD;

takt

$temp := Long.From($left * $mid).Nnmod($MOD),
$temp := Long.From($temp * $right).Nnmod($MOD),
$result := $result + $temp,
$result := $result.Nnmod($MOD),

実装のポイント:

  • 掛け合わせた結果を最終結果に加算します。

結果の例

pgbattle2023_result.png

追加情報

taktコードに利用している計算式ライブラリの関数は以下になります。

For-loopの代替関数:

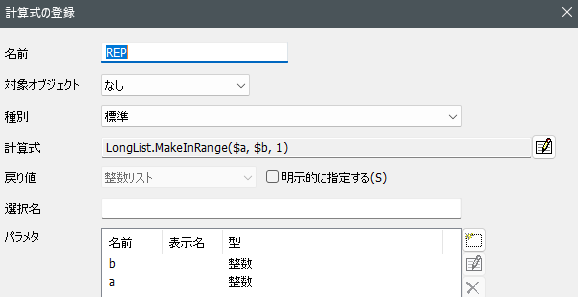
pgbattle2023_rep_func.png

PRINT関数:

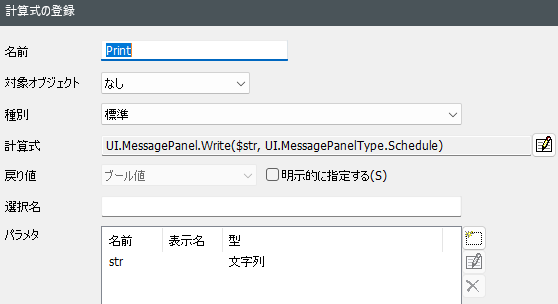
pgbattle2023_print_func.png

デバッグにはUI.MessagePanel.Write関数の使用を推奨します。コメントアウトされている部分を活用することで、デバッグ作業が大幅に便利になります。

全体のコード

c++

#include 
using namespace std;
using ll = long long;
using vvll = vector;
ll MOD = 998244353;

int main(){
    // 入力
    ll N; cin >> N;
    string S; cin >> S;
    // 特殊ケース
    if(N % 2 == 1) {cout << 0 << endl; return 0;}
    // 0. 初期化
    ll N2 = N/2;
    // 1. 組み合わせ数をあらかじめ計算しておく
    vvll Comb(N2+1, vll(N2+1, 1));
    for(int n = 1; n <= N2; n++) 
        for(int k=1; k <= n - 1; k++) 
            Comb[n][k] = (Comb[n-1][k-1] + Comb[n-1][k]) % MOD;
    // 2. メモ化DP: DP[i][j]は[i, j]の区間に選ぶペアの配列数
    vvll DP(N, vll(N, -1)); 
    // 2.1 再帰関数の定義
    function memoization = [&](ll i, ll j){
        if(DP[i][j] >= 0) return;
        if(j - i % 2 == 0) {DP[i][j] = 0; return;}
        ll n = j - i + 1, n2 = n/2;
        ll res = 0;
        // 2.1.1 最後に選ばれるペアを(k, l)とする。ペアで数え上げる。
        // すると区間[i, j]が右のように分けられる [i ... k-1] k [k+1 ... l-1] l [l+1 ... j]
        for(int k = i; k <= j-1; k++) for(int l = k + 1; l <= j; l++){
            if(S[k] == S[l]) continue;
            ll left = 1, mid = 1, right = 1;
            ll nleft = (k - i) /2, nright = (j - l) / 2, nmid = (l - k - 1) / 2;
            // 2.1.2 左・中央・右の区間に対する再帰呼び出し
            if(k > i){
                memoization(i, k-1);
                left = (DP[i][k-1] * Comb[n2 - 1][nleft]) % MOD;
            }

            if(j > l){
                memoization(l+1, j);
                right = (DP[l+1][j] * Comb[n2 - 1 - nleft][nright]) % MOD;
            }

            if(l > k + 1){
                memoization(k+1, l-1);
                mid = DP[k+1][l-1] % MOD;
            }
            // 2.1.3 掛け合わせたものを足し合わせる
            res = (res + ((left * mid) % MOD * right) % MOD) % MOD;
        }
        DP[i][j] = res;
    };
    // 2.2 再帰関数の呼び出し
    memoization(0, N-1);
    cout << DP[0][N-1] << endl;

    // rep(i, 0, N-1) rep(j, 0, N-1) cout << DP[i][j] <<" ";
    // cout << endl;
    return 0;
}

takt

_Print("--- 入力 ---" + String.LF),
_Print($N + String.LF),
_Print($S + String.LF),

$MOD := 998244353,
// 1. 組み合わせ数をあらかじめ計算しておく
$N2 := Math.Max($N.Div(2), 2),
$Comb := LongList.Make(1, ($N2 + 1) * ($N2 + 1), 0),
//_Print("N2: " + $N2 + String.LF),
$GetComb := (Long i, Long j)[$Comb.At($i * ($N2 + 1) + $j)]->Long,
$SetComb := (Long i, Long j, Long val)[$Comb.Set_( $i * ($N2 + 1) + $j, $val)],
_REP(2, $N2).ForEach([
    $m := $_object,
    _REP(1, $m - 1).ForEach([
        $k := $_object,
        $c := $GetComb($m - 1, $k - 1) + $GetComb($m - 1, $k),
        $c := $c.Nnmod($MOD),
        //_Print($m + " " + $k + " " + $c + String.LF),
        $SetComb($m, $k, $c),
    ]),
]),
//_Print("Comb: " + $Comb.ToJSON + String.LF),
// 2. メモ化DP
$DP := LongList.Make(-1, $N * $N, 0),
$GetDP := (Long i, Long j)[$DP.At($i * $N + $j)]->Long,
$SetDP := (Long i, Long j, Long v)[$DP.Set_($i * $N + $j, $v)],
// 2.1 再帰関数の定義
$Memoization := (Long i, Long j)[
    $GetDP($i, $j) >= 0? 0: 
    (
        $len := $j - $i + 1,
        $len2 := $len.Div(2),
        $len.Nnmod(2) = 1?($SetDP($i, $j, 0), 0):(
            $result := Long.From(0),
            // 2.1.1 最後に選ばれるペアを(k, l)とする。ペアで数え上げる。
            // すると区間[i, j]が右のように分けられる [i ... k-1] k [k+1 ... l-1] l [l+1 ... j]
            _REP($i, $j-1).ForEach([ $k := $_object, // k = i, ..., j-1
                _REP($k+1, $j).ForEach([ $l := $_object, // l = k+1, ..., j
                    $S.Substring($k,1) = $S.Substring($l,1)? 0:( // S[k] == S[l] => return;
                        $left := Long.From(1), $right := Long.From(1), $mid := Long.From(1), 
                        $nleft := ($k - $i).Div(2), $nright := ($j - $l).Div(2), $nmid := ($l - $k - 1).Div(2),
                        // 2.1.2 左・中央・右の区間に対する再帰呼び出し
                        $k > $i ? (
                            $Memoization($i, $k - 1),
                            $left := $GetDP($i, $k - 1) * $GetComb($len2 - 1, $nleft),
                            $left := $left.Nnmod($MOD),
                        1 ): 0,
                        $j > $l ? (
                            $Memoization($l + 1, $j),
                            $right := $GetDP($l + 1, $j) * $GetComb($len2 - 1 - $nleft, $nright),
                            $right := $right.Nnmod($MOD),
                        1 ): 0,
                        $l > $k + 1? (
                            $Memoization($k + 1, $l - 1),
                            $mid := $GetDP($k + 1, $l - 1).Nnmod($MOD),
                        1 ): 0,
                        // 2.1.3 掛け合わせたものを足し合わせる
                        $temp := Long.From($left * $mid).Nnmod($MOD),
                        $temp := Long.From($temp * $right).Nnmod($MOD),
                        $result := $result + $temp,
                        $result := $result.Nnmod($MOD),
                    )
                ])
            ]),
            $SetDP($i, $j, $result),
            1
        ),
        1
    )
]->Long,
// $ans := Long.From(-1),
// 2.2 再帰関数の呼び出し
$Memoization(0, $N - 1),

$ans := $GetDP(0, $N - 1),
_Print("--- 出力 ---" + String.LF),
_Print($ans + String.LF)

LongList.MakeInRange($a, $b, 1)

｜スタッフブログトップに戻る｜

ユーザー

購読する このブログを購読

PAGETOP