takt式マニアクス③ モンティ・ホール問題をFLEXSCHEでシミュレーション
モンティ・ホール問題とは
「モンティ・ホール問題」を知っていますか?
米国のモンティ・ホールという司会者の番組で行われたゲームに由来するそうです。
その概要は以下の通りです。
3つの閉じた扉がある。 そのうち1つの扉はアタリで、回答者は、その扉を選んだ場合、扉の裏にある商品を獲得できる。 ただし、回答者が扉を選ぶと司会者はその扉を開ける前に、他の(ハズレの)扉を開けてみせ、さらに、回答者に、選ぶ扉を変更してもよいと告げる。 回答者は、選ぶ扉を変更すべきか?
皆さん、どう思いますか?
ちなみに、米国のマリリンという女性がこの問題について尋ねられ、「選ぶ扉を変える方が2倍得」と答えたところ、大論争が巻き起こったとのこと。
私はこの問題を「ラスベガスをぶっつぶせ」という映画で知りました。その時、私の取った行動は「FLEXSCHEのtakt式でシミュレーションして確認する」でした。さて、その結果は・・・
takt式でモンティ・ホール問題をシミュレーション
ということで、私がどのようにして確認したかを説明することにします。
アタリ扉の決め方
まず、商品のある扉をランダムに決める仕組みが必要です。そのために、目が1から3までの「サイコロ」を用意しましょう。
これはtakt式の乱数を発生させる機能で実現できます。具体的には、
Long.Random(1,3)
という式で実現できます。この式は、1~3のうちのどれかの整数を、ランダムに同じ確率で返します。
これが返した値を、アタリ扉の番号、とします。
$existing := Long.Random(1,3)
次に、回答者が最初に選ぶ扉の番号をどうするかですが、これはどれを選んでも同じ(でいいですよね?)なので、常に1番を選ぶことにしましょう。
$firstAnswer := 1
選ぶ扉を変えない場合
選ぶ扉を変えない場合、最終的な回答 $finalAnswer は
$finalAnswer := $firstAnswer
ということになります。
これがアタリかどうかは、$existing と $finalAnswer が一致するかどうか、です。ここで条件演算子
<A>?<B>:<C>
を使います。これは、<A>の式が真ならば<B>の式の値を、偽ならば<C>の式の値を返す、というものです。したがって、
($existing = $finalAnswer) ? 1 : 0
という式は、アタリの場合は1、ハズレの場合は0を返すことになります。
ここまでの式をつなぎましょう。複数の式を連続して実行するには、各式を , (半角カンマ)でつなげばよいです。
$existing := Long.Random(1,3), $firstAnswer := 1, $finalAnswer := $firstAnswer, ($existing = $finalAnswer) ? 1 : 0
ただし、1回だけ試してもよくわかりませんね。1万回繰り返して、アタリの回数を合計しましょう。
そのために、サイズが1万のリストを生成します。
LongList.Make(1,10000)
アタリの回数を合計するには、Sum関数を使えばよいです。
LongList.Make(1,10000).Sum([ ])
この[ ] の中に式を書けば、その式を1万回計算した結果の合計が、最終的な計算結果となります。というわけで、
LongList.Make(1,10000).Sum([ $existing := Long.Random(1,3), $firstAnswer := 1, $finalAnswer := $firstAnswer, ($existing = $finalAnswer) ? 1 : 0 ])
と書けばよさそうです。FLEXSCHEで実際に試してみると、
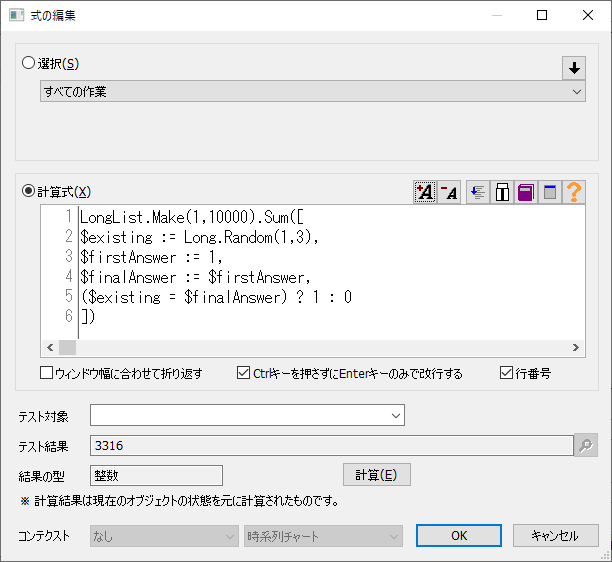
計算結果は「3316」となりました。
結果は毎回変化しますが、だいたい3333近辺になります。
つまりアタリの確率は約1/3ということです。まあこれは当然ですね。
選ぶ扉を変える場合
では、回答者が選択を変える場合はどうなるでしょうか。
ここでも同様に、回答者はまず1番を選ぶと答えることにしましょう。司会者は2番か3番のどちらかを開けて見せることになります。
ここで司会者の立場になって、どちらを開けるかを考えると、正解の扉がどれかによって状況が異なることがわかります。
もしも1番が正解なら、司会者は2番と3番のうちどちらを開けてもよいことになります。実際にどちらを選ぶかは個人的な好みが反映されるかもしれませんが、このシミュレーションではランダムに選ぶことにします。
もしも2番が正解なら、司会者は2番を開けるわけにはいかないので、3番を開けることになります。
もしも3番が正解なら、司会者は2番を開けることになります。
回答者は、いずれの場合も、司会者が2番を開けたら3番を、3番を開けたら2番を最終的な回答とすることになります。
これらをtakt式で表現すると、以下のようになります。
$existing := Long.Random(1,3), $open := ($existing = 1 ? Long.Random(2,3) : ($existing = 2 ? 3 : 2) ), $finalAnswer := ( $open = 2 ? 3 : 2 ), ($existing = $finalAnswer) ? 1 : 0
これを1万回繰り返した時のアタリの合計を算出する式は、
LongList.Make(1,10000).Sum([ $existing := Long.Random(1,3), $open := ($existing = 1 ? Long.Random(2,3) : ($existing = 2 ? 3 : 2) ), $finalAnswer := ( $open = 2 ? 3 : 2 ), ($existing = $finalAnswer) ? 1 : 0 ])
ですね。実際にFLEXSCHEで試してみると
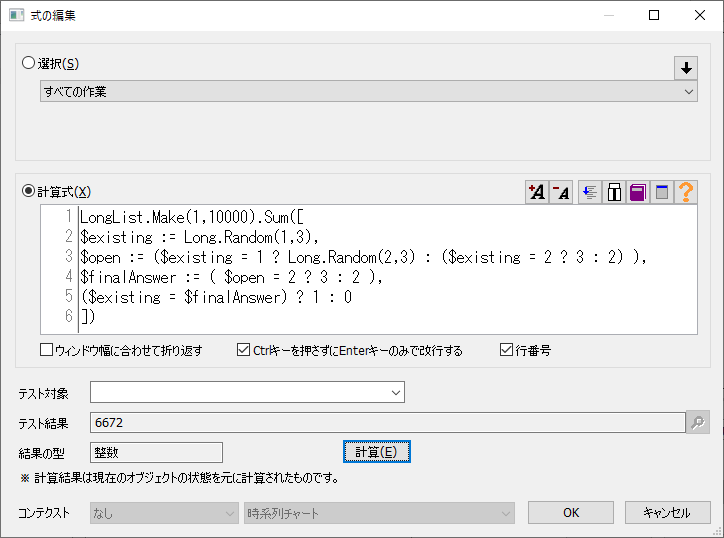
6672となりました。この値も毎回変化しますが、だいたい6666近辺になります。率でいえば約2/3、変えない場合のほぼ倍です。
というわけで、マリリンさんの言う通り、という結果になりました。
どうしてこうなるの?
選ぶ扉を変える場合、なぜこのような結果になるのでしょうか?
察しの良い方は既にお気付きかもしれませんが、上で
もしも1番が正解なら、司会者は2番と3番のうちどちらを開けてもよいことになります。実際にどちらを選ぶかは個人的な好みが反映されるかもしれませんが、このシミュレーションではランダムに選ぶことにします。
もしも2番が正解なら、司会者は2番を開けるわけにはいかないので、3番を開けることになります。
もしも3番が正解なら、司会者は2番を開けることになります。
回答者は、いずれの場合も、司会者が2番を開けたら3番を、3番を開けたら2番を最終的な回答とすることになります。
と述べました。ここがポイントです。
回答者が「選択を変える」と決めた場合、回答者には選択肢が残っていません。司会者が2番を開けたら3番を、3番を開けたら2番を選ぶだけです。
そして、正解が1番の場合、司会者が2番を開けようが3番を開けようが、どちらにせよ回答者が選ぶ残りの一つはハズレです。
逆に、正解が1番でない場合、司会者は(慎重に)正解でない方を開け、残りを回答者が選ぶので、最終的には必ずアタリになります。
| 正解の扉 | 最初の選択 | 司会者が開ける扉 | 最終的な選択 | 最終結果 |
| 1 | 1(アタリ) | 2または3 | 3または2 | ハズレ |
| 2 | 1(ハズレ) | 3 | 2 | アタリ |
| 3 | 1(ハズレ) | 2 | 3 | アタリ |
つまり、最初の選択が正解なら最終的にはハズレ、逆に不正解なら最終的にアタリ、となるのです。
正解の扉が1、2、3のどれになるかは、いずれも確率1/3なので、「選択を変える」作戦の場合、最終的なアタリの確率は2/3ということになります。
応用問題(その1)
では、扉がもっと多い場合はどうなるのでしょうか?
具体的には、扉が4つで、アタリは1つだけで、司会者が開けてみせる扉は2つ、だとします。
| 正解の扉 | 最初の選択 | 司会者が開ける扉 | 最終的な選択 | 最終結果 |
| 1 | 1(アタリ) | 2~4のうち2つ | 2~4のうち開いていないもの | ハズレ |
| 2 | 1(ハズレ) | 3と4 | 2 | アタリ |
| 3 | 1(ハズレ) | 2と4 | 3 | アタリ |
| 4 | 1(ハズレ) | 2と3 | 4 | アタリ |
こうなると、司会者が正解を教えてくれているかのようですね。
この場合、選ぶ扉を変えるならアタリ確率は3/4、変えないなら1/4、となります。変える方が3倍得ということですね。
応用問題(その2)
では、扉が4つで、アタリは1つだけなのは同じだけれど、司会者が開けてみせる扉は1つ、の場合はどうなるでしょうか?
この場合は、少し複雑になります。場合分けすると以下の通りです。
| 正解の扉 | 確率 | 最初の選択 | 司会者が開ける扉 | 部分的な確率 | 最終的な選択 | 部分的な確率 | 最終結果 | 最終確率 | ||
| 1 | 1/4 |
1 (アタリ) |
2~4のうち1つ | 1 | 2~4のうち開いていないものどれか | 1 | ハズレ | 1/4(=1/4*1*1) | ||
| 2 | 1/4 |
1 (ハズレ) |
3または4 | 3 | 1/2 | 2または4 | 2 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) |
| 4 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
| 4 | 1/2 | 2または3 | 2 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) | ||||
| 3 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
| 3 | 1/4 |
1 (ハズレ) |
2または4 | 2 | 1/2 | 3または4 | 3 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) |
| 4 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
| 4 | 1/2 | 3または2 | 3 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) | ||||
| 2 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
| 4 | 1/4 |
1 (ハズレ) |
2または3 | 2 | 1/2 | 4または3 | 4 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) |
| 3 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
| 3 | 1/2 | 4または2 | 4 | 1/2 | アタリ | 1/16(=1/4*1/2*1/2) | ||||
| 2 | 1/2 | ハズレ | 1/16(=1/4*1/2*1/2) | |||||||
結局、選ぶ扉を変える場合にアタリとなる確率は、最終結果が「アタリ」の行の最終確率を合計して、(6/16=)3/8となります。
選ぶ扉を変えない場合は1/4(=2/8)なので、この場合は、変える方が少し得、ということになりますね。
まとめ
先入観を排除して順番に段階を追って実現していくと、大論争を巻き起こした問題に対しても明確な結論に到達できる、というのは、なかなか面白いですね。
ちなみに、このように、確率的な問題を乱数を用いたシミュレーションで解く方法を「モンテカルロ法」と言います。「モンティ・ホール問題」に限らず、内容によってはFLEXSCHEでも試せるので、機会があったら是非トライしてみてください。

